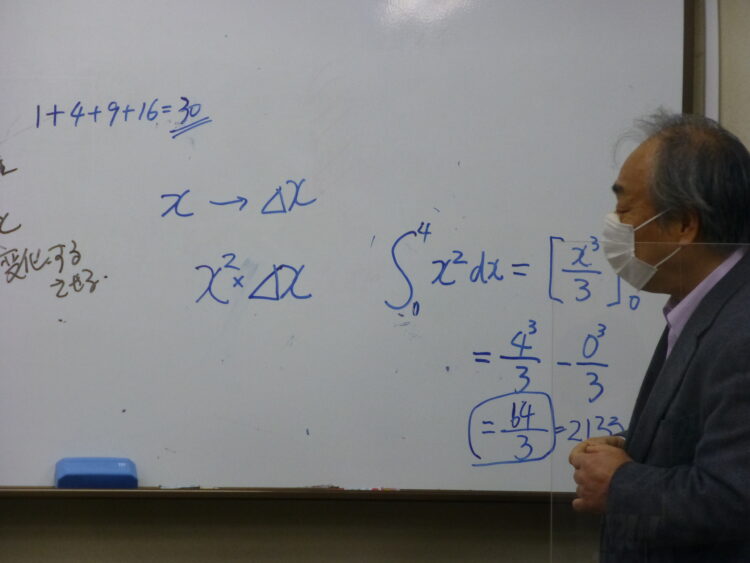奥田孝一大学校長が、学生に難しくない理数科的なお話をする特別講座「おもしろ理数科」。6名の学生の参加を得て、最終回となる第6回目を開催しました。

1　開催日時

令和3年11月16日(火)　16:15〜17:00

2　開催場所

兵庫県立但馬技術大学校　本館2階　センター教室2

3　講師

兵庫県立但馬技術大学校　大学校長　奥田孝一

4　講座の様子

　今回は、これまでの統計・確率から離れて微分と積分がテーマに。参加した学生たちも、微分や積分が苦手という人も多かった様子でした。
まずは、微分と積分の概念の説明です。微分は「細かく分ける・分割する」との意味。積分は「積み合わせる・合計する」との意味とのことです。

　　

　まず、葉っぱの面積を求めるには、どうすればいいでしょうか？方眼紙の上に置いて、少しでも方眼紙にかかっているものを１として合計すれば、正確ではないけどまずまずの値の面積が求められます。方眼紙のマス目を小さくすればするほど正確な面積が求められますが、現実的には限りがあります。しかし、数学の世界では無限小、すなわち限りなくゼロに近い細かさに分割することができるのです。簡単に言えばこれが微分ということであり、細かく分けたもの(無限の断片)を足し合わせて面積を求めることが積分といえます。

　　

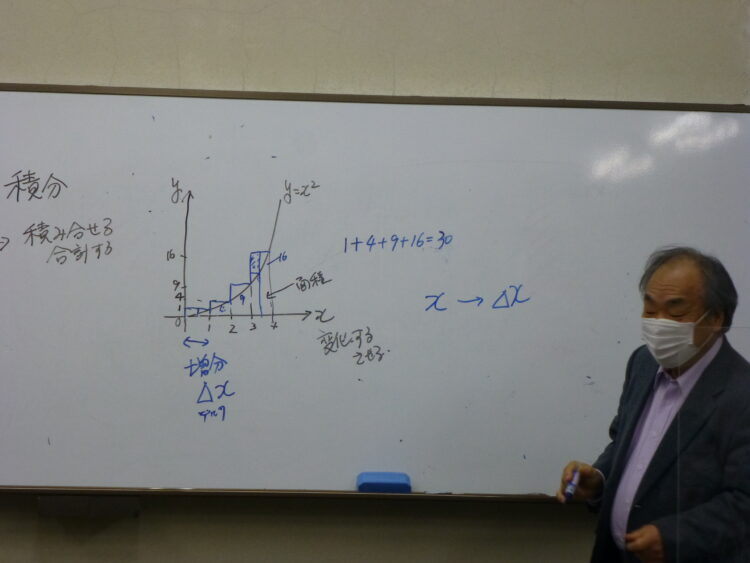
　少しだけ数学の教科書的な話をします。例えばy=x^2のグラフ(放物線)とX軸で囲まれる面積(x=0～4)はどのように求めればいいでしょうか。先の話のように放物線を細かく分けてみましょう。とりあえず4等分して幅が１の長方形の集まりとしましょう。それぞれの面積は１×１、１×４、１×９、１×１６となるのですべてを合計すると３０になります。でもこの値は、放物線の上にはみ出したところだけ実際の面積より大きくなっています。長方形の幅を０.５にすればはみ出し部分の面積は小さくなります。教科書で習う微分・積分では、長方形の幅を限りなく０として足し合わせることで正確な面積(厳密解)を求めます。

　　

　数学の教科書では、こんなふうにインテグラルの記号式で計算しましたね。覚えているでしょうか。厳密解は６４/３、およそ２１.３３３・・・となります。当然ですが幅１で計算した３０より、だいぶ小さな値ですね。

　　

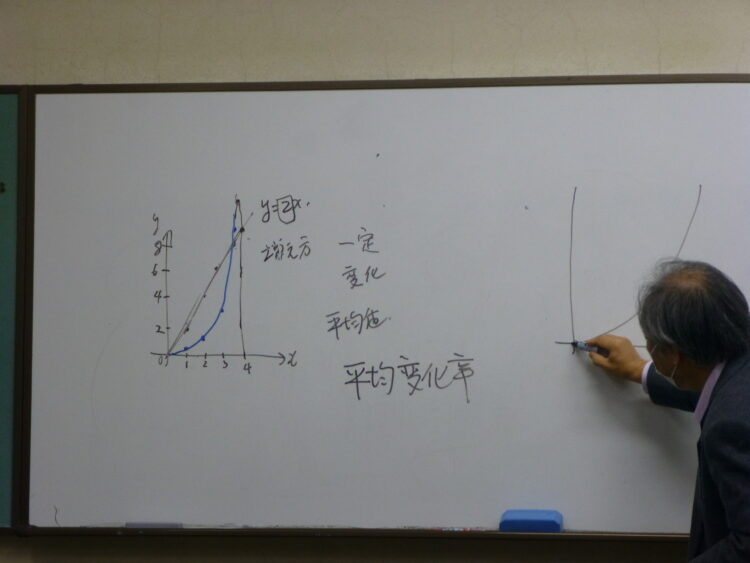
　最初に微分は細かく分けることと言いましたが、変化の程度、度合いを表しています。例えば、y=2xの直線ではｘが１増えるとｙは常に２増えるように一定の割合で変化します。一方、y=x^2の放物線では変化の仕方は一定ではありませんが。ｘが０から１に１増えるとｙは０→１、２から３に１増えるとｙは４→９に増えます。それぞれの変化量１と５のことを平均変化率(２点を結ぶ直線の傾き)と習いましたね。ｘの増分を１から小さくしていって限りなく０に近くすると、その直線は放物線の１点で接することとなりこれを接線といいます。この接線の傾きをｘのある値における微分係数と言い、ｙ’とかdy/dxで表しましたよね。

今回が今年度の最終回となります。また、来年も企画しますので、是非、ご参加ください。